Algoritmos de búsqueda

05 JULY 2020

Linear search (búsqueda secuencial).

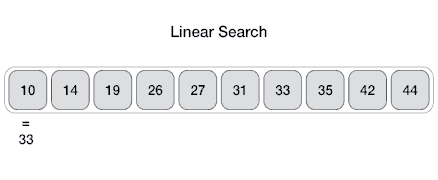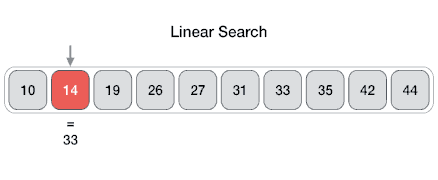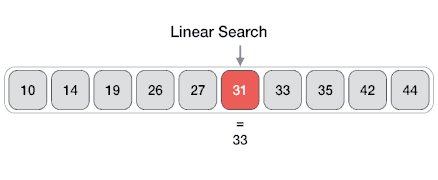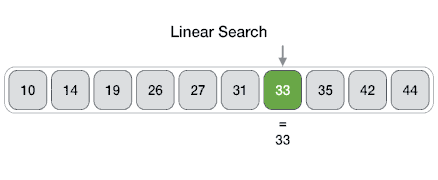
• Complejidad \(O(n)\) (en el peor de los casos se hará un número de comparaciones igual al tamaño del elemento).
• Es el algoritmo de búsqueda más sencillo.
• Busca un elemento en una lista o un vector.

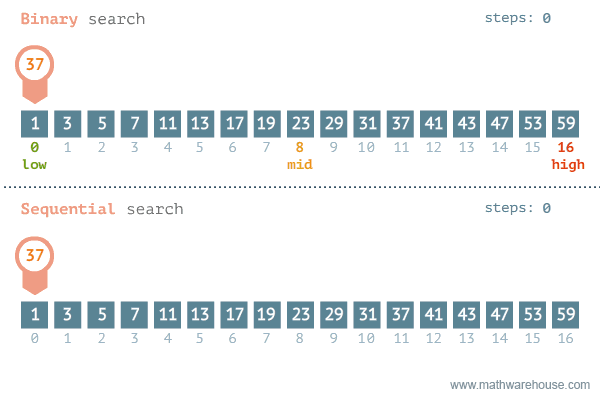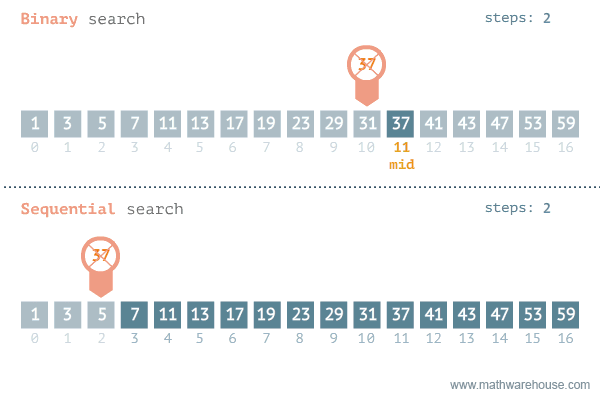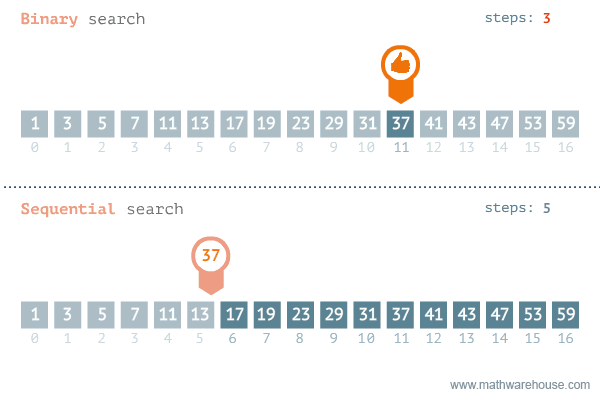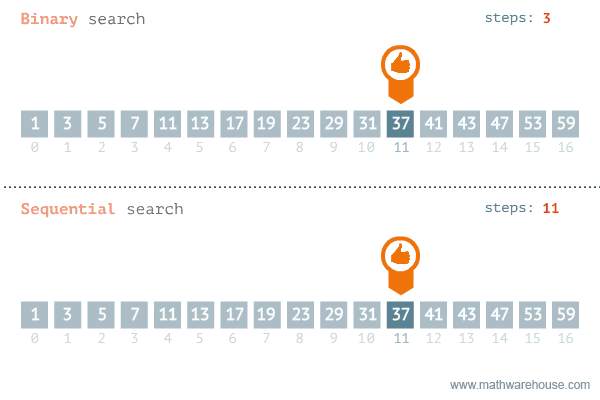
Binary Search (búsqueda binaria).

• Busca un número en un arreglo ordenado.
• Compara el elemento buscado con el central.
• Si el central es el elemento buscado, termina.
• Si el central es menor que el buscado, se realiza la búsqueda en la mitad supeior.
• Si el central es mayor, se realiza la búsqueda en la mitad inferior.

Interpolation search (interpolación).

• Complejidad \(O(n)\).
• Modificación de binary search.
• El código es prácticamente el mismo, a excepción del cálculo del elemento central.
• En cada etapa, trata de calcular dónde está el elemento central (con un pivote) usando la fórmula:

\[\ middle = low + \frac{ (buscado - a[low]) (high - low)}{a[high] - a[low]}\]

En este visualizador se puede observar el desarrollo del algoritmo.

Hashing (Hash).

• Mapea grandes data sets a unos más pequeños.
• Provee una forma de búsqueda rápida.
• Determina una función de Hash que permite buscar y encontrar un índice para una llave.

\(\ f(llave)\) —–> índice único

• Se puede aplicar en encriptación (SHA -256 o MD5).
• La forma más básica de un Hash es la función identidad.
• La función ideal es inyectiva y biyectiva, pero es muy difícil de hallar.

Técnicas de Hash:

• Restas sucesivas.
• Aritmética modular.
• Cuadrado medio.
• Truncado.
• Folding.

Colisiones:

• Una colisión es cuando una función tiene la misma imagen para distintas preimágines. Es decir, dos o más llaves tienen el mismo índice.
• Una tabla hash con muchas llaves es un causante de colisiones.
• Es difícil de evitar.

Aquí se puede leer un artículo sobre el hash con el fin de aclarar más la definición y algunos usos en la encriptación de contraseñas y seguridad. Demasiado interesante, súper recomendado para leer.

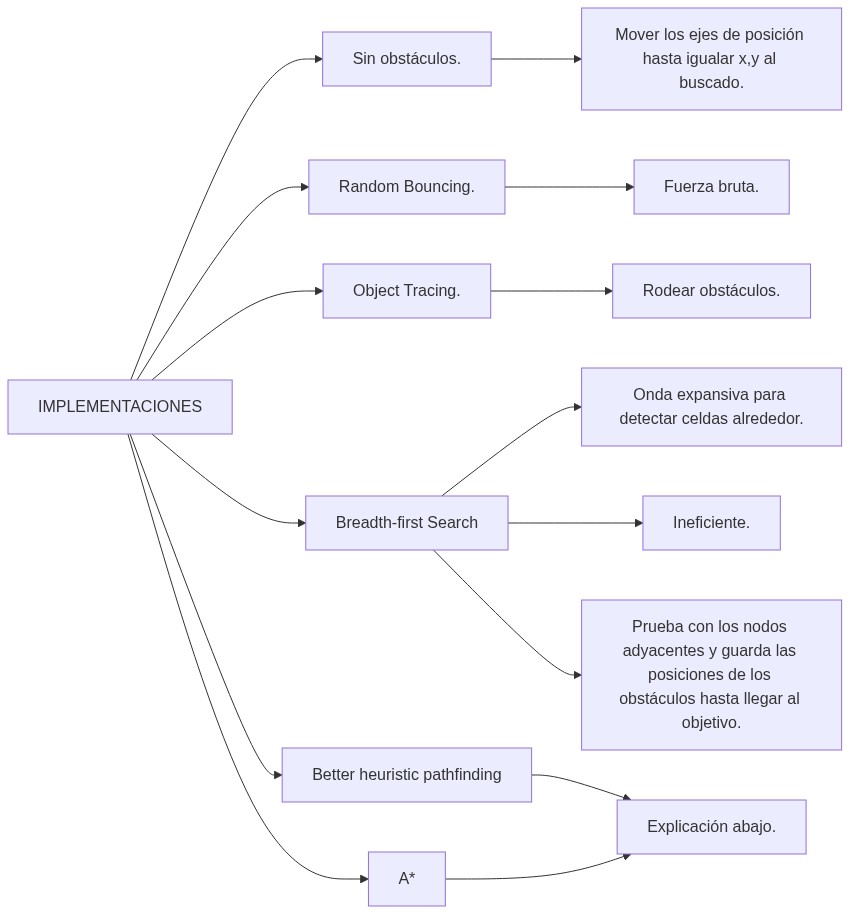
Pathfinding.

Aquí se puede acceder a una vista dinámica del esquema.

El Pathfinding es la búsqueda de la ruta más corta entre dos puntos mediante métodos computacionales. Está basado en el algoritmo de Dijkstra.

El procedimiento se caracteriza por:

• Explora los nodos adyacentes y selecciona los más cercanos.
• Trabaja sobre una matriz, cada celda es un nodo.
• Es capaz de resolver laberintos.

Existen diferentes algoritmos para implementar el pathfinding. A continuación se muestran algunos.

Los algoritmos Better Heuristic y A* son un poco más complicados e importantes. Por esto, se desarrollan un poco más.

Better Heuristic Algorithm (algoritmos heurísticos).

El término heurístico se utiliza cuando se hace referencia a una optimización de un algoritmo. En este caso, el pathfinding. Esta idea está más desarrollada Northwestern University Open Text Book on Process Optimization que lo describen así:

A heuristic algorithm is one that is designed to solve a problem in a faster and more efficient fashion than traditional methods by sacrificing optimality, accuracy, precision, or completeness for speed.

Es muy importante destacar que para alcanzar el objetivo de optimización es posible que se sacrifiquen aspectos como: exactitud o presición. Esto porque el enfoque es la velocidad.

Se concentra en tomar la mejor decisión, es decir, que tarde menos tiempo en cálculos para la obtención de la ruta más corta. No encontrará la ruta más óptima pero sí algunas de las más cortas.

El término, en la computación, también se utiliza para desribir soluciones más “inteligentes” que las originales.

Algunos de los algoritmos heurísticos más conocidos son:

• Swarm intelligence (inteligencia de enjambre).
• Artificial neural networks (redes neuronales).
• Genetic algorithms (algoritmos genéticos).

Estos algoritmos se pueden aplicar en el escaneo de virus en una computadora y como algoritmos de búsqueda y ordenamiento.

A* (A star).

Este es un algoritmo conocido por ser preciso, rápido y confiable. Se utiliza mucho en el desarrollo de videojuegos.

Como es un algoritmo derivado del principio del pathfinding, hace uso de una matriz para el cálculo de rutas. Las celdas las divide de la siguiente manera:

• Red wall.
• Blue goal.
• Green start.
• id: caminado / no caminado.

El proceso para entender este algoritmo lo explica Computerphile en su canal, pero recomiendo ver el video del algoritmo de Dijkstra primero.

A modo de resumen, la diferencia principal entre el algoritmo de Dijkstra y A* es:

Dijkstra: Es expansivo (busca todas las rutas posibles).

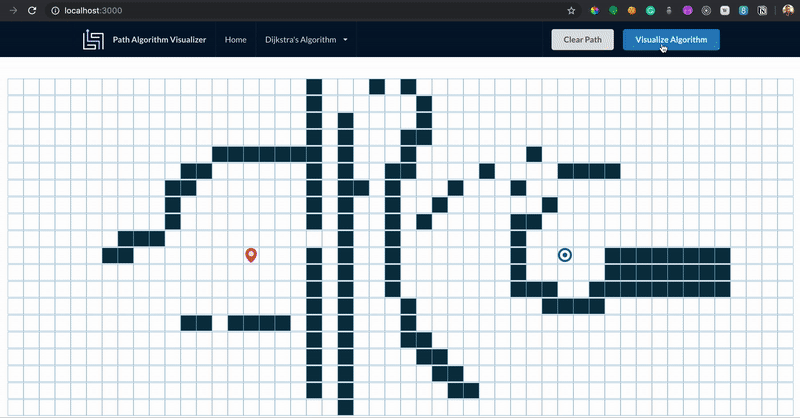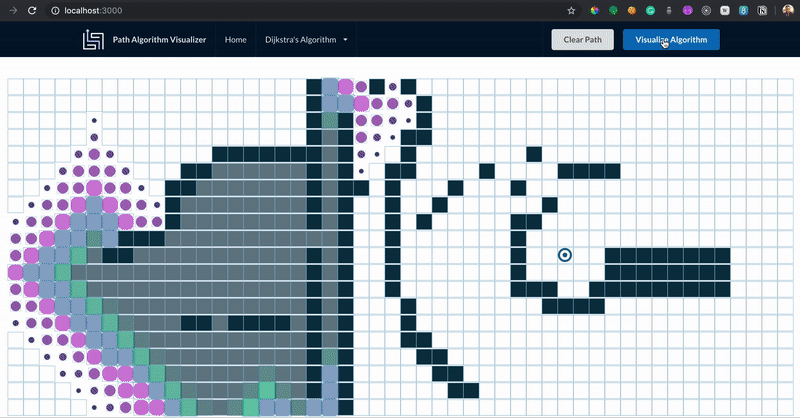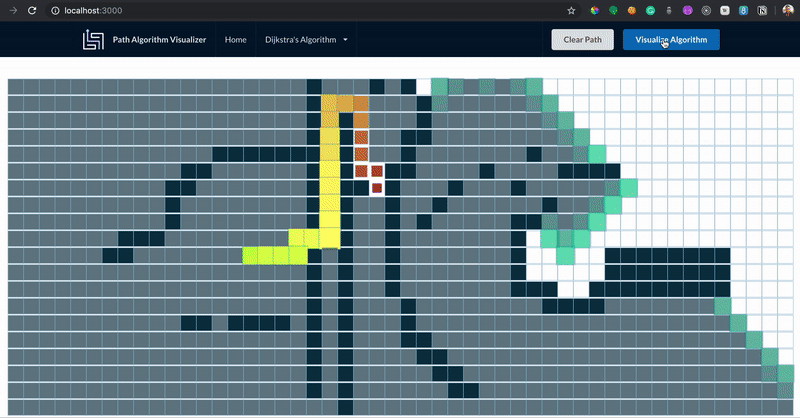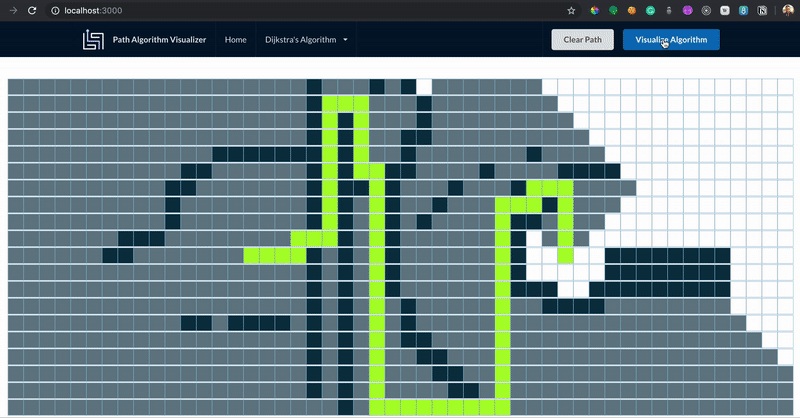
A star: Es selectivo (escoge gradualmente las rutas más efectivas).

Aplicar este algoritmo implica conocer los principales cálculos, como lo indica Graph Everywhere, donde también se puede encontrar un ejemplo de apliación y un poco de historia:

Para la aplicación de este algoritmo debemos comprender como se procede a dividir el costo de la ruta. En este caso se divide en dos partes donde \(g(n)\) representa el costo de la ruta desde su origen hasta algún nodo n dentro del grafo. También tenemos que \(h (n)\) representa el costo estimado de la ruta desde el nodo n al nodo de destino, calculado por una suposición inteligente.

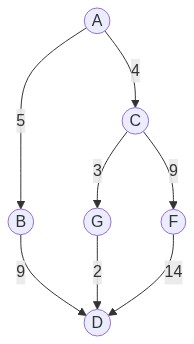
Por ejemplo: En el siguiente grafo, el nodo origen sería A y el nodo destino es D.

Entonces, algunos valores \(g(n)\) serían:

• Del nodo C: \(g(n) = 4\).
• Del nodo B: \(g(n) = 5\).
• Del nodo F: \(g(n) = 13\).
• Del nodo G: \(g(n) = 7\).

Por lo tanto, \(g(n)\) básicamente es el valor que cuesta llegar a un nodo por la suma de las aristas. Luego, \(h(n)\) es un valor aproximado. El método para calcular este valor varía según su aplicación. Por ejemplo, si fuera una aplicación de rutas como Google Maps entonces una posibilidad es que se calcula la línea recta (en metros) desde un nodo hasta el nodo destino.

Para este ejemplo definiré \(h(n)\) de la siguiente manera: el mínimo de aristas faltantes para llegar al nodo. Entonces algunos valores quedarían así:

• Del nodo C: \(h(n) = 2\).
• Del nodo B: \(h(n) = 1\).
• Del nodo F: \(h(n) = 1\).
• Del nodo G: \(h(n) = 1\).

Ahora, el único valor faltante sería \(f(n)\) el cual se define como \(f(n) = h(n) + g (n)\) Por lo tanto, los valores quedarían así:

• Del nodo C: \(f(n) = 6\).
• Del nodo B: \(f(n) = 6\).
• Del nodo F: \(f(n) = 14\).
• Del nodo G: \(f(n) = 8\).

El objetivo que se obtenga el \(f(n)\) más bajo posible. Para ver una expliación sobre un proceso completo de A* recomiendo este video.