Análisis de algoritmos

02 JULY 2020

Aquí se puede acceder a una vista dinámica del esquema.

A modo de resumen, un algoritmo es una serie de pasos finitos bien definidos que solucionan un problema. Se pueden representar mediante varias técnicas como el pseudo-código o los diagramas de flujo y sus principales características son:

• Finito.
• Determinístico.
• Preciso.
• Correcto.

¿Qué es el análisis de algoritmos?**

Es una metodología que permite estimar el consumo de recursos computacionales de un algoritmo. Este se analiza con el fin de evaluar si puede ser aplicado en otros contextos. También, para clasificar problemas de acuerdo a su dificultad, compararlos y optimizarlos.

Se evalúa espacio de memoria, tiempo computacional y procesadores que el algoritmo consume. Algunos factores que afectan la eficiencia son:

• Developer.
• Tamaño del input.
• Compilador.
• Sistema Operativo.
• Lenguaje.
• Sistema (CPU, memoria, disco).
• Los procesos corriendo en el computador.

Ahora, tres modelos para medir la eficiencia de los algoritmos:

1. Empírico.
   • Se utilizan Benchmarks para hacer mediciones.
   • Generar archivos comprimidos y ver cuál ocupa más espacio.
2. Simulacional:
   • Se utilizan datos de un simulador.
   • Se incluyen casos de prueba (diferentes inputs).
   • No se puede simular por completo, falta de tiempo.
3. Analítico:
   • Modelos matemáticos.
   • Es el más exacto pero el más complejo a la vez.

Complejidad computacional.

Existe la Teoría de la complejidad computacional que pretende analizar los algoritmos desde el punto de vista de los recursos computacionales. Alan Turing sentó las bases para este tema ya que su Máquina de Turing es la única conocida capaz de analizar todos los algoritmos. En Medium escriben una pequeña reseña histórica sobre el tema.

La complejidad es estimada por conteo de instrucciones elementales. Estas son operaciones de la computadora cuyo tiempo es despreciable (tardan lo mismo en todos los computadores). Por último, analiza la tasa de crecimiento de la función según el tiempo o el espacio.

Complejidad computacional de tiempo.

Consiste en un método de análisis de algoritmos que se realiza mediante el conteo de instrucciones elementales. Existes dos tipos: tiempo real o de pared y de reloj. Por ejemplo, el de reloj consiste en medir según la frecuencia a la que corre el procesador (Hz, o GHz).

Instrucciones elementales.

• Toman el mismo tiempo independientemente del tamaño del input.
• El tiempo de ejecución se denota mediante la variable T.
• Tipo de operaciones:
  • Aritméticas: suma, resta, divisiones, etc.

  • Bit operations: «, », &,

    .

  • Lógicas: ==, !=, &,

    .

  • Jumps: return, llamadas a métodos, etc.
  • Asignaciones, accesos a arrays.

Conteo de instrucciones.

A continuación se muestran algunos ejemplos para el conteo de instrucciones.

A) Complejidad de un for básico. La complejidad de un for se denota como O(2n+2) y se justifica así:

for (i=0;   //------> 1 asignación: 1T  
	 i<n;   //------> n+1 comparaciones: T(n+1) 
	i++)	//------> n incrementos: Tn
			//Total-> 1T + T(n+1) + Tn = T(2n+2)

B) Complejidad de un for no básico. La complejidad de un for como el ejemplo siguiente se denota como O(n+1). En este caso el incremento del contador se da en dos unidades por lo tanto se recorre la mitad de los datos solamente.

for (i=0;   //------> 1 asignación: 1T  
	 i<n;   //------> (n/2)+1 comparaciones: T[(n/2)+1] 
	i+=2)	//------> n/2 incrementos: T(n/2)
			//Total-> 1T + T[(n/2)+1] + T(n/2) = T(n+1)

Aquí puede encontrarse una explicación más amplia y con ejemplos adicionales sobre análisis de algoritmos fundamentales.

Análisis asintótico.

Dada una función obtenida mediante conteo de instrucciones, el análisis asintótico se enfoca en encontrar el término que determina el crecimiento de la función.

\(T(n) = 2n^3+\ 3n^2 +\ log(n) +\ 333\) El término más importante es el que indica el grado de la función y los demás son despreciables.

Por lo tanto, según el análisis asintótico:

\[T(n) = n^3\]

Este análisis se puede realizar enfocándose en:

• Peor caso (suele ser suficiente).
• Caso promedio.
• Mejor caso.

Big \(O\) (omicron)

• Encontrar el peor caso.
• Encuentra la cota superior.

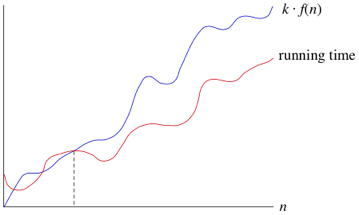
Si el peor caso es \(\kappa \ f(n)\), se comporta linealmente, cualquier caso va a ser igual o mejor que este. Por debajo de esta línea se encuentran todos los casos posibles representados por la función running time.

Big \(\Theta\) (theta)

• Encontrar la cota superior e inferior a partir de cierta cota.

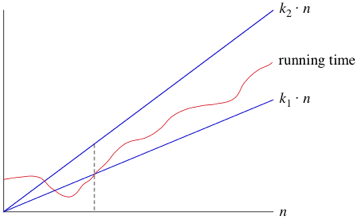
\(\kappa_1n\) corresponde a la cota inferior y \(\kappa_2n\) a la superior, mientras que la función running time es el espacio para los posibles comportamientos.

Big \(\Omega\) (omega).

• Encontrar el límite inferior.

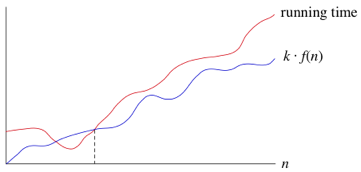
\(\kappa \ f(n)\) corresponde a la cota inferior y la función running time sería los posibles casos.

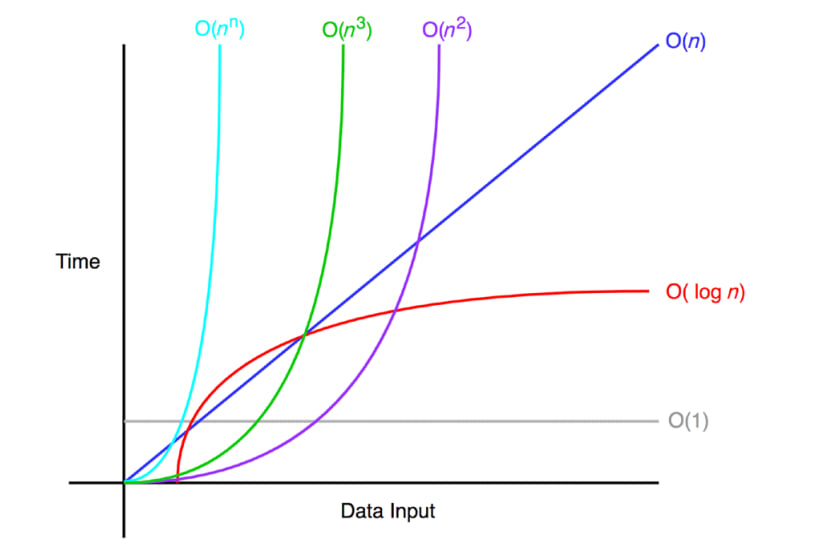
Órdenes de crecimiento comunes.

• Constante \(\ k\).
• Logarítmica \(\ Log(n)\) // —> Estos logaritmos son base 2 por convención computación.
• Lineal \(\ n\).
• Lineal logaritmica \(\ nLog(n)\).
• Cuadrática \(\ n^2\).
• Cúbica \(\ n^3\).
• Exponencial \(\ k^n\).
• Factorial \(\ n!\) .