Diseño de algoritmos

10 JULY 2020

El diseño consiste en el planeamiento de un producto cuyo fin es es mostrar la apariencia y funciones de un objeto antes de su construcción.

El proceso del diseño de algoritmos lleva algunos pasos significantes:

• Formular el problema con suficiente precisión matemática.
• Concretar la pregunta y comenzar a pensar en algoritmos para solucionar.
• Diseñar el algoritmo para el problema.
• Analizar el algoritmo para verificar si es correcto.
• Evaluar la eficiencia del resultado.

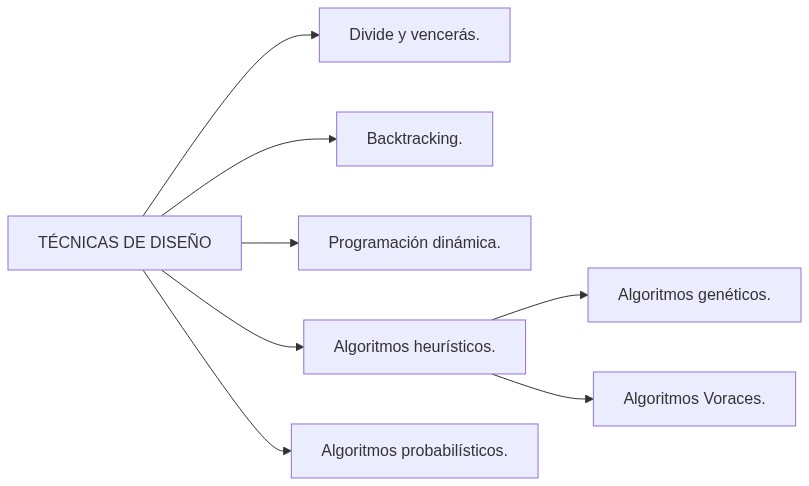
Ahora bien, este proceso de formulación de algoritmos se complementa de algunas técnicas de diseño particulares. Familiarizarse con ellas lleva su tiempo pero con la experiencia se vuelve más sencillo solucionar problemas. Algunas categorías de técnicas de diseño son:

Divide y vencerás (Divide and Conquer).

El proceso se interpreta de forma literal a su nombre. Tal como se aprecia en el siguiente ejemplo gráfico sobre el algoritmo de ordenamiento merge sort:

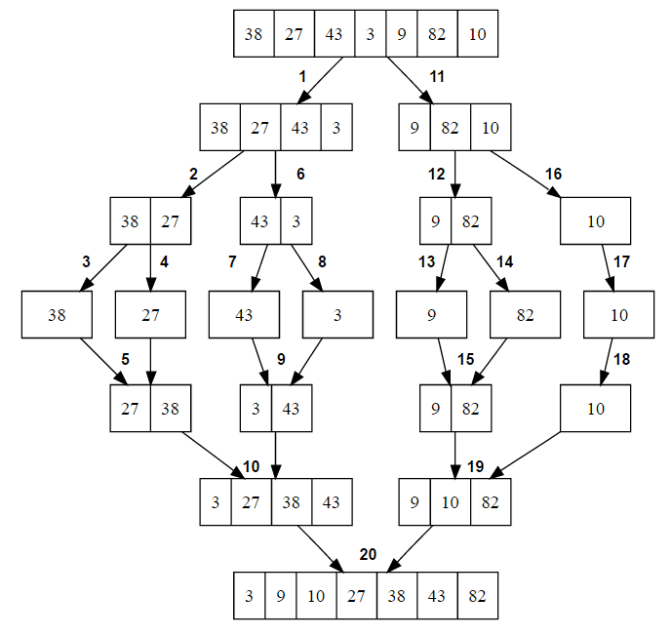
El proceso se puede resumir de la siguiente manera:

1. Dividir el problema en subproblemas.
2. Conquistar los subproblemas de forma recursiva.
3. Combinar las soluciones.
4. Al alcanzar el problema más pequeño posible, se definen los casos base y se trabaja a partir de ahí.
5. Es altamente eficiente.

Este principio busca múltiples soluciones de forma paralela.

Khan Academy explica más este tema.

Algunos algoritmos que utilizan Divide y vencerás son:

• Quicksort.
• Strassen’s Algorithm: multiplica dos matrices.
• Karatsuba Algorithm: permite multiplicar números muy grandes usando pequeñas tres multiplicaciones pequeñas.

Backtracking.

El backtracking consiste en una técnica para probar secuencias de decisiones hasta encontrar la correcta. Puede terminar sin una solución.

La técnica de backtracking prueba decisiones y si encuentra una incorrecta entonces se devuelve. Parecido a caminar en un laberinto.

Cuando caminamos por un laberinto y topamos con un camino cerrado (solución incorrecta) entonces nos devolvemos hasta la último camino correcto y escogemos otra ruta (recursivamente). Este es el principio del backtracking.

Las soluciones se pueden ver como un árbol de decisiones. Esto nos da un indicativo de que este algoritmo es recursivo.

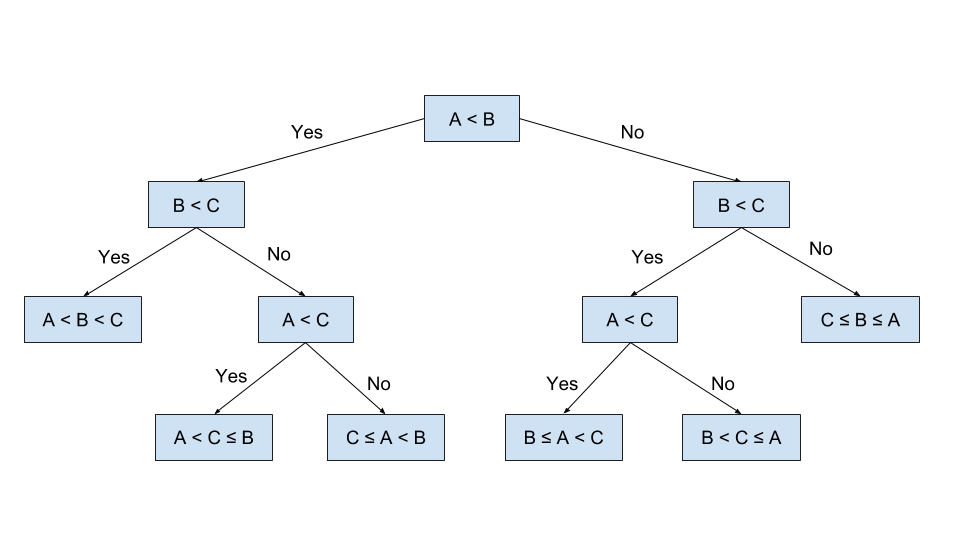
En gestión de operaciones lo definen así:

Es un método analítico que a través de una representación esquemática de las alternativas disponible facilita la toma de mejores decisiones, especialmente cuando existen riesgos, costos, beneficios y múltiples opciones. El nombre se deriva de la apariencia del modelo parecido a un árbol y su uso es amplio en el ámbito de la toma de decisiones bajo incertidumbre (Teoría de Decisiones) junto a otras herramientas como el Análisis del Punto de Equilibrio.

Los árboles de decisiones se caracterizan por:

• Plantear una pregunta en un nodo.
• Las ojas de esa raíz se convierten en soluciones.
• Los árboles básicos se plantean de forma binaria. Donde la hoja izquierda es 1 y la derecha 0.

Si un nodo conduce solo a errores, se retorna al nodo padre y se evaluan otros nodos. Encuentra todas las soluciones posibles. Se usa en lenguajes como Prolog.

En caso de que te interese GeekForGeeks hizo una lista de las principales 20 preguntas sobre Backtracking en entrevistas de trabajo.

Algunos problemas clásicos del backtracking son:

• Sudoku.
• N Queens Problem.
• Letter combination phone.
• The Knight’s Tour Problem.
• Coloring Graph Problem.

N Queens Problem (problema de las n reinas).

Consiste ubicar las $n$ reinas en una matriz de $n*n$ sin que se relacionen en la misma diagonal, horizontal o vertical.

Debido a que este problema se amplía mucho al desarrollarlo, recomiendo ver el siguiente video:

Aquí se puede acceder al código y la explicación.

Letter combination phone.

Dado un string que contiene dígitos [2, 9] inclusivo. Retorne todas las posibles combinaciones de las letras que representa cada uno de los dígitos.

Por ejemplo:

> Input: "23"
Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

Programación dinámica.

Método para resolver problemas dividiéndolos en problemas más simples, con el fin solucionar problemas más complejos.

Algunas características son:

• Subestructura óptima: cada solución de un problema es óptima.
• Overlapping de problemas: el espacio de los subproblemas debe ser pequeño y se tiene que resolver el mismo subproblema una y otra vez.
• Se diferencia de Divide y vencerás porque se reutilizan los resultados.
• Cada vez que se soluciona un problema se guarda el resultado en una tabla.
• Al solucionar un problema nuevo, se revisa la tabla y si no está entonces proceso y guardo la solución.

But unlike, divide and conquer, these sub-problems are not solved independently. Rather, results of these smaller sub-problems are remembered and used for similar or overlapping sub-problems.

Tal como lo indica Tutorials Point la principal característica que tienen los problemas en que se implementa este proceso es el problema se debe poder dividir en subproblemas similares. Es así como este diseño de algoritmos se vuelven eficientes. Además, son algoritmos de optimización.

Estos son algunos ejemplos clásicos que se pueden resolver usando programación dinámica:

• Fibonacci number series.
• Knapsack problem.
• Tower of Hanoi.
• All pair shortest path by Floyd-Warshall.
• Shortest path by Dijkstra.
• Project scheduling.

Algoritmo de la mochila (0-1 the Knapsack Problem).

Se tiene una mochila con un máximo de peso con el que se puede cargar. Todos los productos disponibles tienen un valor de precio y peso. Consiste en un problema de optimización. Es decir, ganar el mayor valor posible dentro del peso aceptado.

En el siguiente artículo de medium desarrollan de forma muy clara la aplicación de la programación dinámica para resolver este problema.

La torre de Hanoi (Tower of Hanoi).

Consiste en que se tienen tres ejes en los que se colocan aros circulares con diferentes diámetros. Solamente un aro de menor diámetro por encima de otro de mayor. Todos los aros comienzan en el eje más izquierdo y el participante debe pasarlos al eje derecho siguiente la condición de orden. También trata de un problema de optimización.

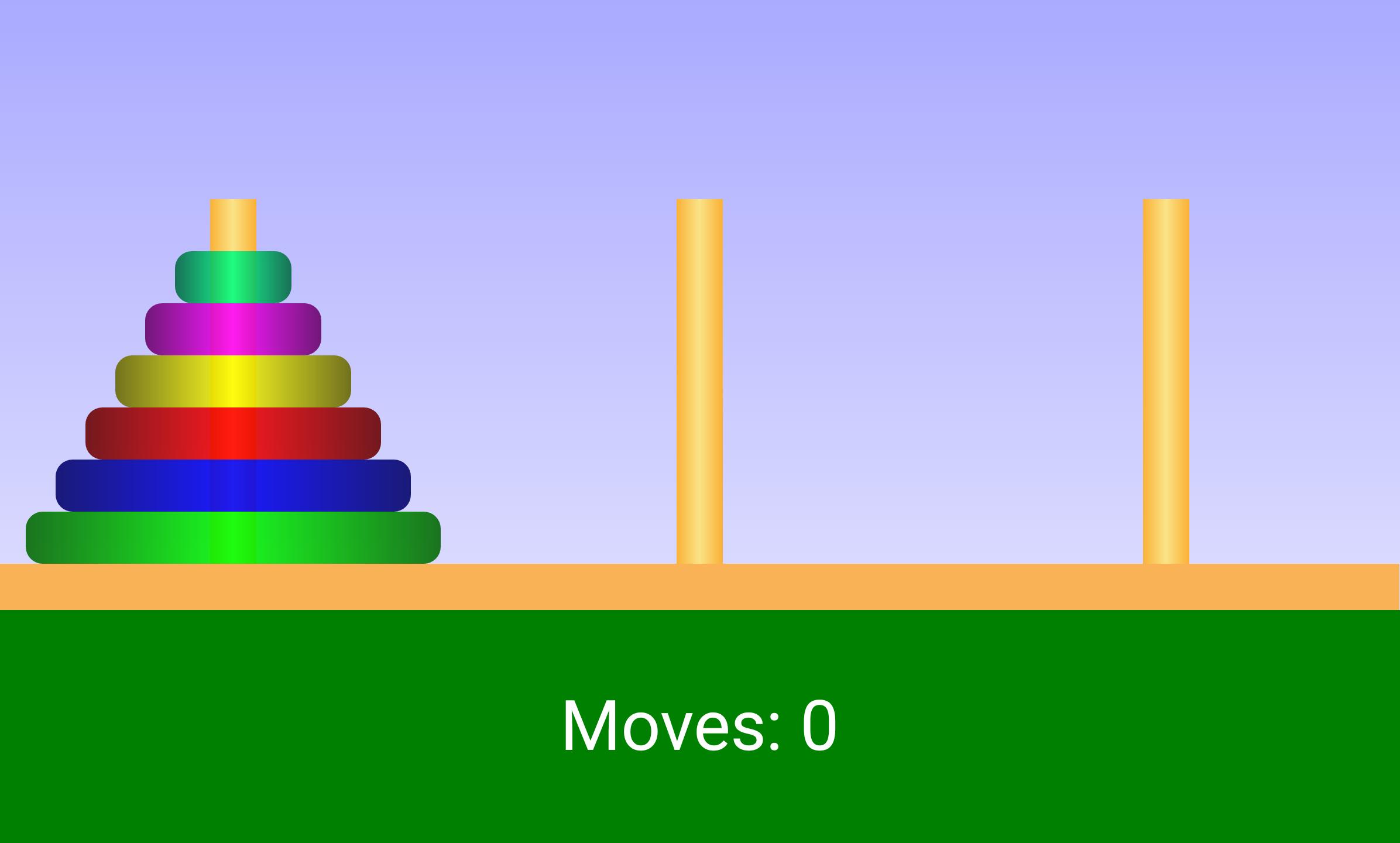
Recomiendo muchísimo jugar Tower of Hanoi. Es un gran ejercicio para la lógica.

Se puede encontrar mucha información al respecto pero edpresso lo resume muy bien.

Heuristic Algorithms (heurísticos).

Estos algoritmos que se caracterizan por garantizar que están muy cerca de ser óptimos. Se utilizan en escenarios donde la precisión puede ser sacrificada por rendimiento.

Algunos ejemplos son:

• Genetic algorithms.
• Greedy algorithms.

Genetic algorithms (algoritmos genéticos).

Los algoritmos genéticos consisten en un tipo de búsqueda heurística basada en la teoría de Darwin que dice que el que sobrevive es el que tiene las mejores características para adaptarse al medio, y combina esa idea de la evolución con la genética. Se basa en la utilización de mecanismos que imitan a la evolución biológica para formular los pasos a seguir.

En caso de tener interés en repasar la teoría de evolución de Darwin, este video explica la historia.

Es una técnica robusta y puede tratar con éxito una gran variedad de problemas provenientes de diferentes áreas. Aplicaciones en sistemas de computación paralelos, química, negocios y comercio (modelización de sistemas económicos complejos, predicción de mercados), entre otros.

Fue desarrollado por Dr. John Henry Holland (1929 - 2015). Un pionero en sistemas complejos y ciencia no lineal. También es conocido como el padre del Algoritmo genético. Profesor de Filosofía, de Ingeniería Eléctrica y de Ciencias de la computación en la Universidad de Míchigan.

En la naturaleza todo el proceso de evolución se hace de forma natural. Aplicar esta idea a la solución de problemas conlleva algunas implicaciones en la población generada:

• Tamaño.
• Diversidad.

Estos dos factores son fundamentales ya que permiten la correcta generación de las mutaciones entre generaciones.

Representa una exploración aleatoria usando información histórica de las generaciones para dirigir la búsqueda. Se busca una función fitness que se encarga de crear una nueva generación con los cambios correspondientes.

Algunas definiciones importantes son:

• Cell: contiene los cromosomas (cadena ADN).
• Chromosome: conjunto de genes (bloques de ADN).
• Genotype: colección de genes responsables de un rasgo.
• Reproducción: combinación de genes padre.
• Mutación: alteraciones durante la reproducción.
• Fitness: cuánto se puede reproducir antes de morir.

En este video se muestra un excelente ejemplo de los algoritmos genéticos. Donde se crean generaciones de carros con ciertas características. Estas van evolucionando usando “the fittest car” como base. Este término “the fittest” se utiliza para hacer referencia al individuo de mayor éxito de cierta generación.

El proceso de los algoritmos genéticos se puede resumir en:

1. Generar una población base. Puramente aleatoria.

2. Selección. Tras evaluar la generación, es decir mandar los individuos a la guerra, se aplica la función fitness para escoger quienes se pueden reproducir.

3. Crossover. Reproducir los individuos seleccionados por cruce. Se reproducen entre ellos.

4. Mutaciones. Se mutan algunas características de la generación base con el fin de incrementar la segunda población.

5. Mezclar. Se combina la población que se origina de los cruces con la población originada tras mutar la población base.

6. El algoritmo termina cuando no se puedan generar individuos significativamente diferentes. Entonces se dice que el algoritmo ha propuesto un set de soluciones al problema. Sino se continua con el ciclo.

Hay varios aspectos que son importantes a la hora de implementar este algoritmo:

• El tamaño de la población depende del problema.
• Una población pequeña puede crear un máximo limitante pero una población demasiado grande requiere de muchos recursos computacionales.
• Para las reproducciones se define un padre y una madre.

Vijini Mallawaarachchi desarrolla un poco más los algoritmos genéticos y muestra un ejemplo en código.

Algunos problemas clásicos en los que se utilizan estos algoritmos son:

• Travelling Salesman Problem.
• Cashier Problem.

Greedy algorithms (algoritmos voraces).

Los algoritmos voraces usan la filosofía de construir una solución a partir de pequeños pasos. En cada paso toma una decisión que los lleva gradualmente a una decisión final. Estos algoritmos siempre escogen la opción que se ve mejor en el momento. Esto quiere decir que una decisión local óptima se espera que lleve a una decisión global óptima.

En algunos casos, esta meta no es alcanzada y la solución final no es óptima. Igualmente, se obtiene una aproximación. Aún así, son algoritmos rápidos.

Los principales componentes son:

1. Set de candidatos. A partir de este se creará la solución.

2. Selección. Esta función escoge los mejores candidatos para agregarlos a la solución.

3. Factibilidad. Esta función se utiliza para determinar si un candidato puede ser utilizado para contribuir a la solución.

4. Objetivo. Corresponde a la función encargada de asignar un valor a la solución global o parcial.

5. Solución. Se encarga de indicar cuándo se ha finalizado con la solución global.

Algunos problemas en los que se aplican algoritmos voraces son:

• Dijkstra Algorithm.
• Find largest sum.
• Cashier Algorithm.
• Kruskal and Prim Minimum Spanning Tree.
• Huffman Coding.
• Traveling Salesman Problem.

Algoritmos probabilísticos.

Esta consiste en una técnica de diseño de algoritmos en la cual se utilizan números al azar para decidir qué hacer. Requieren de demasiados recursos computacionales para encontrar una solución óptima.

Inclusive con el mismo input, estos algoritmos varían su comportamiento en cada ejecución.

Categorías:

• Numéricos:
  • Solución aproximada.
  • 90% de probabilidades de dar una solución correcta.
  • Cuanto más se ejecuta más se incrementa la probabilidad.
• Las Vegas:
  • Toma decisiones random.
• Monte Carlo:
  • Calcula la mejor solución de un alto grado de probabilidad.
  • Cuanto más se ejecuta más se incrementa la probabilidad.

En caso de querer ampliar el tema: science4all.

Ejemplos de algoritmos de este tipo:

• Hashing.
• Sorting.
• Searching.
• Load Balancing.
• Minimum spanning trees.
• Shortest paths.